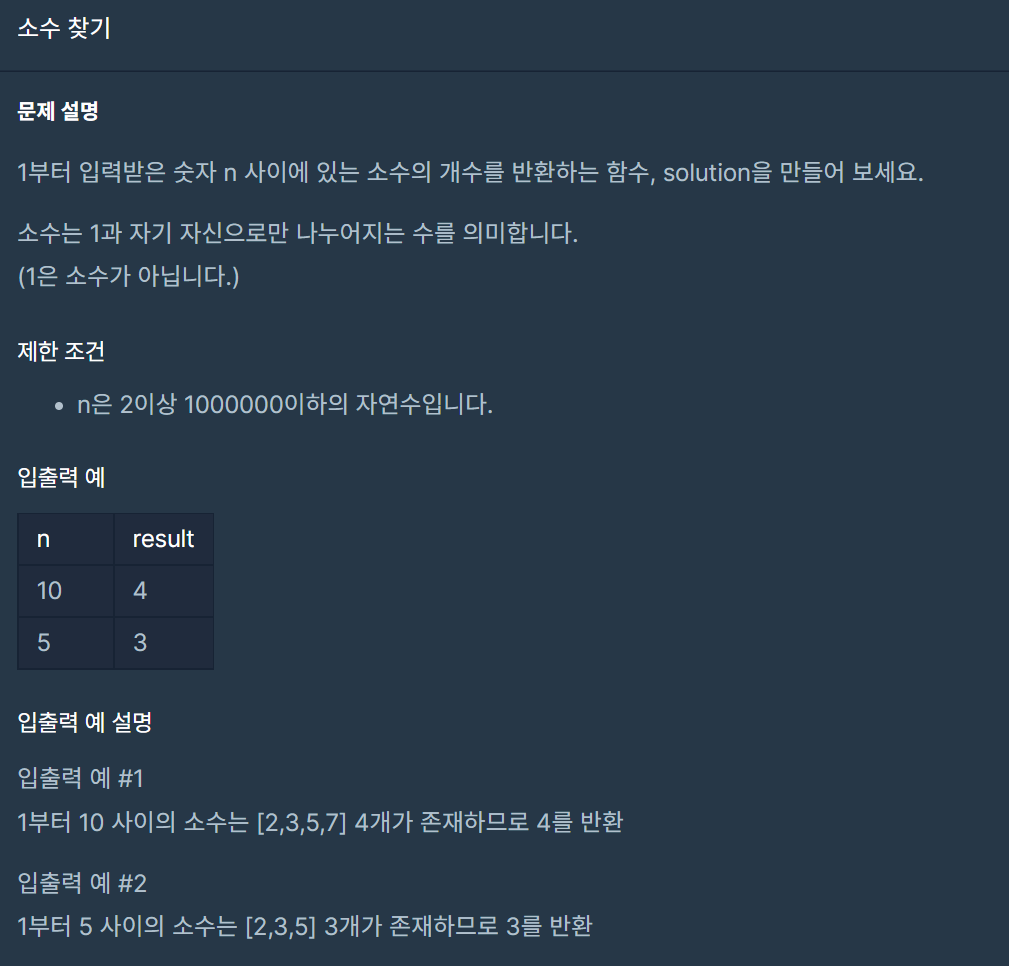
1. 문제 설명
2. 문제 풀이 핵심이라 생각하는 점
- 소수의 개념
- 효율성에 대한 참고
- 에라토스테네스의 체
3. 정답 코드 확인 및 활용 메소드 체크
3-1 : 소수는 1과 자기자신만 약수를 가지는 수
class Solution {
public int solution(int n) {
int count = 0;
int answer = 0;
for(int i = 1 ; i <= n ; i++){
for(int j = 1 ; j <= i ; j++){
if ( i % j == 0) count++;
}
if(count == 2) answer++;
count = 0;
}
return answer;
}
}
3-2 : 에라토스테네스의 체 사용
- 배열에 있는 숫자가 j로 나누어떨어지면 소수가 아니기 때문에 flag를 false로 바꾸어준다.
- lag가 그대로 true라면 소수라는 뜻이므로 숫자를 카운트해 줘서 소수의 개수를 찾을 수 있다.
class Solution {
public int solution(int n) {
int answer = 0;
boolean[] sosu =new boolean [n+1];
for(int i=2; i<=n ; i++)
sosu[i]=true; //2~n번째수를 true로 초기화
//제곱근 구하기
int root=(int)Math.sqrt(n);
for(int i=2; i<=root; i++){ //2~루트n까지 검사
if(sosu[i]==true){ //i번째의 수가 소수일 때
for(int j=i; i*j<=n; j++) //그 배수들을 다 false로 초기화(배수는 소수가 아니기 때문)
sosu[i*j]=false;
}
}
for(int i =2; i<=n; i++) {
if(sosu[i]==true) //소수의 개수 세기
answer++;
}
return answer;
}
}
1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
2. 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
3. 자기 자신을 제외한 2의 배수를 모두 지운다.
4. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
5. 자기 자신을 제외한 3의 배수를 모두 지운다.
6. 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
7. 자기 자신을 제외한 5의 배수를 모두 지운다.
8. 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
9. 자기 자신을 제외한 7의 배수를 모두 지운다.
10. 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
참고한 곳
프로그래머스 - 소수찾기 [java]
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.
velog.io
3-3 : 효율성을 위한 조언 참고
- 정수론에 대해서 공부하지 않으면 쉽게 생각하기 힘들 수 있습니다.
- 일단 여기서는 간단히 3가지 수학 정리만 소개하겠습니다.
- 1보다 큰 모든 자연수는 소수의 곱으로 이루어져 있다.
이것은 가장 기본적인 정리입니다. 이 정리가 의미하는 바는 무엇일까요? - 대부분의 사람들은 소수를 구하기 위해서 2부터 차례대로 증가시켜서 나누어보는 방법을 이용할 것입니다. 그러나 이 방식은 굉장히 비효율적입니다. 그렇지만 1보다 큰 자연수는 소수의 곱으로 이루어져 있기 때문에 소수로만 나누면 됩니다.
- 예를 들어서, 10이 소수인지 아닌지를 알기 위해서 10보다 작은 소수만을 이용하면 됩니다. 실제로 10보다 작은 소수는 4개입니다. 그러니깐 4개만 이용하면 됩니다. 그리고 100이 소수인지 아닌지를 알기 위해서 99개의 자연수를 모두 이용한 것 대신에 25개의 소수만 이용하면 됩니다.
- 어떤 자연수 n이 있을 때, √n 보다 작은 모든 소수들로 나누어 떨어지지 않으면 n은 소수입니다.
언뜻 이해하기 힘들겠지만 한 번 이해하면 쉽습니다. 증명을 생략하고 예를 들겠습니다. 먼저 101이 소수인지 아닌지 판별하기 위해서 우리는 √101을 구하면 10.xxx이 됩니다. 자 10보다 작은 소수는 뭐가 있을까요? 일단 2, 3, 5, 7이 있습니다. 그런데 딱 봐도 이 4개의 소수로만 101이 나누어 떨어지지 않습니다. 그러므로 101은 소수입니다. 위의 방식을 이용하면 25개의 소수를 모두 이용해야 하지만 지금은 4개만 이용해도 쉽게 계산이 됩니다. - 2보다 큰 모든 짝수는 어차피 합성수입니다. 어차피 2로 나누어 떨어지기 때문이죠. 이 방식은 사용하지 않았습니다. 저는 위의 2가지 방식만을 이용해서 효율성 테스트를 통과했습니다.
'Programmers > JAVA' 카테고리의 다른 글
| [ 프로그래머스 ] 최소 직사각형 - Java (0) | 2023.01.14 |
|---|---|
| [ ArrayList 생성 ], [ ArrayList 메소드 ], [ ArrayList ↔ List 변경 ] (0) | 2023.01.14 |
| [ 프로그래머스 ] 가장 가까운 같은 글자 - Java (0) | 2023.01.13 |
| [ 프로그래머스 ] JadenCase 문자열 만들기 - Java (0) | 2023.01.10 |
| [ 프로그래머스 ] 마법의 엘리베이터 - Java (0) | 2023.01.06 |